Imaginary Numbers for Dummies
Imaginary/complex numbers explained for the math curious
Following is an easy-to-understand explanation of imaginary numbers (and by extension, complex numbers — the distinction will be explained) suitable for the mathematically… disinclined, shall we say?
A full understanding of the real numbers is not necessary. We will deal only with the integers (the whole, or “counting" numbers plus their opposites, and zero). If you’re fraction-phobic… no worries. No fractions or decimals are necessary to fully understand the concepts.
We start at the very beginning, and assume nothing, and we end… not at the end, but at the end of the beginning: a basic comprehension of what is meant by an imaginary number.
Prep
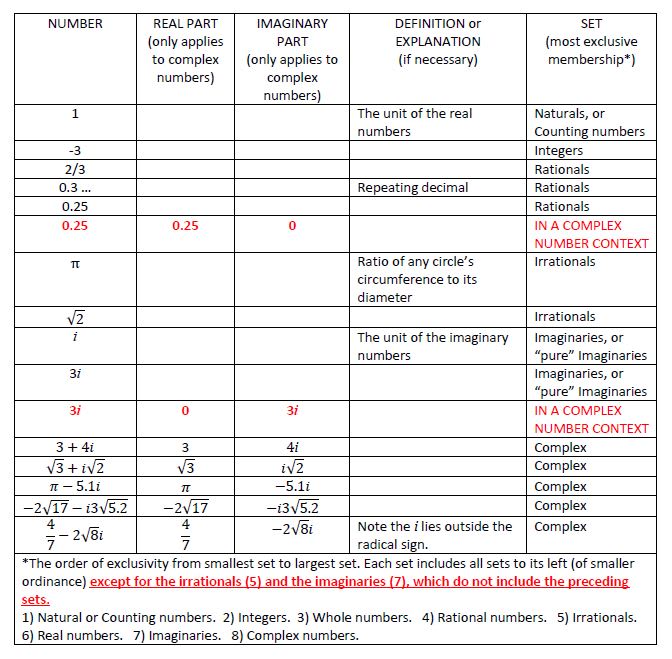
The number 1 is the unit of the real numbers. The real number system incorporates all the numbers other than imaginaries (i.e. the imaginary numbers). That means all the familiar numbers used in everyday life (specifically, the integers, fractions, and decimals, as well as the irrational numbers[1]). The number 1 is the unit of the real numbers because all other countable quantities are expressed as amounts of … it. For example, how many 1s are there in 5?
Pro tip: there are 5.
As I said, the number system we will use for this exercise is the whole numbers. The whole numbers include all the counting, or natural numbers plus their opposites, aka their negatives — plus zero.
Let’s first talk about the sign rules of the arithmetic operations on the whole numbers, avoiding any esoterica about zero because it doesn’t play into the goal of this exercise, understanding imaginary numbers.
Arithmetic means using addition, subtraction, multiplication or division on numbers. When using arithmetic with real numbers we are always counting. I use counting here in the sense of producing a measurable quantity. The calculation may not produce an integral quantity. If we divide 1 by 3 we do not get a whole number such that we could say “there are 2 of them,” or 7 of them. But we get a quantity that is measurable (in this case, the fraction 1/3 … sorry about that… I said we wouldn’t need to mention fractions… I lied).
Also, we have to account for a measurable quantity that results is an absence of a quantity, such as -3 (“negative-three of them”). Negative-three is a deficit. Three more needs to be found somewhere to make up the deficit. Hence, -3.
If only positive numbers are involved, the result of any series of arithmetic operations must result in another positive number. It is only when a negative number is part of a calculation that the result of a calculation may turn out to be a negative number.
When a positive is added to a negative the result can be either positive or negative (or zero). Similarly with subtraction. This is because we are counting quantities and the absence of quantities. In addition, if the positive quantity exceeds the negative (i.e., the amount is greater than the absence of an amount), the result will be positive. If the reverse is true, the sum will be negative.
If a positive number is multiplied with a negative, the result will be negative. We can justify this by thinking of it as adding up a bunch of negatives – you only get more negatives.
The sign rules for division work the same as multiplication. (They are inverse operations; they undo each other, just as with addition and subtraction.)
What about the multiplication (or division) of two negative numbers? Though visualizing what this means in terms of counting can be difficult, we don’t have to stress about it because there is only one possibility: it must produce a positive number. Why? Because it cannot produce a negative number. Let’s assume it could and we immediately see the logical contradiction.
Given 2 x -3 = -6. How could -2 x -3 also equal -6? Compare them.
If 2 x -3 = -6 and also -2 x -3 = -6, this clearly implies that 2 must equal -2. Which of course it doesn’t — unless we’re in Star Trek…
Thus the product (answer from a multiplication) or the quotient (answer after division) of two negative numbers must produce a positive number.
Operations with real numbers always produce another real number. When working with physically countable quantities (in the loose sense I am using it; see above) we must get another measurable quantity. [Zero is a valid amount here.]
Now we are ready to enter the realm of these strange numbers, the imaginary numbers.
The imaginaries
Exponentiation is the name for raising a number to a power. It is a compact form for a specific kind of multiplication, when a number is multiplied by itself. If the number 5 is multiplied by itself 4 times, using arithmetic that would be written 5 x 5 x 5 x 5. Exponentiation was invented to shorten this process. With it, we say “5 to the fourth power,” which is written mathematically like this: 54. Four is called the exponent, and 5 is called the base.
For our purposes we only need to consider raising to the second power, which is referred to as squaring. For example, the quantity 52 is verbalized as “five-squared.”
[52 = 25, because 5 x 5 = 25.]
All mathematical operations have an inverse operation. Subtraction is the inverse of addition (and vice-versa); division is the inverse of multiplication (and vice-versa). The inverse of squaring is taking the square root. The radical symbol, √, is used to denote a square root. As we note from above, since 5-squared is 25, the square root of 25 must be 5.
Important: Though this is clearly true, it is not complete. As we showed above, a negative times a negative also yields a positive number. While 5 x 5 produces 25 – so does -5 x -5. This means that there is another square root of 25: -5.
Indeed, there will always be two square roots to any positive number, one positive and one negative.
Are you ready? Here we go…
What about the square root of a negative number?
We’ve already determined that the only way that two numbers can multiply to a negative number is if they are opposite in sign: one positive, the other negative. That means they cannot be the same number. That means there can be no square root of a negative number … in the real numbers, the world of measurable quantities.
All the operations we have discussed so far involve quantities that are physically measurable, even if they are “absences” of quantities (i.e. negative numbers).
What do we do? We could say that there is no such thing as the square root of a negative number and be done with it. And indeed, there is no measurable meaning to it. But we go ahead anyway. Why? Because math.
What we do is we define a new set of numbers. We appropriately call them imaginary, because in the sense of using numbers to count things in the real world, they serve no obvious function.
We start by defining a unit for this new set of numbers, a number from which all other imaginaries can be constructed, as in, every imaginary number corresponds to some amount of the unit. We choose the square root of the negative of the unit of the real numbers, that is, the square root of -1:
We name this unit “i”.
Somewhat surprisingly, we define this imaginary unit, i, not as the square-root of -1, but as “the number whose square produces -1.” Operationally there is no difference between these definitions. We casually say “i is the square root of -1,” and no one will raise an eyebrow if you say that, but technically “i is the number that when squared equals -1.” Don’t worry about this.
Quantities of i are written with a (real) number next to it, like 5i. This means five is, 5 multiples of i, or 5 times i. Such a number is sometimes identified as a pure imaginary number. The i can be after or before the real number, so i5 is the same as 5i. Don’t worry about this either.
Complex numbers
Now to the distinction between imaginary numbers and complex numbers.
Since the middle of the 19th century, it’s all about sets. As we have mentioned, the real numbers is a set of numbers. It is the largest set of numbers used to observe and measure our physical world. Imaginary numbers are outside the set of real numbers. When these two sets are combined, the superset created out of them is called the complex numbers. Note that any single real or imaginary number is considered to be in the set of complex numbers. The following numbers are all in the complex numbers: 0, 1, 2/3, 7.39, 1.66666…, π, i, 2.3i.
Of these, all but i and 2.3i are real numbers. i and 2.3i are imaginary numbers, also referred to as pure imaginaries.
But generally speaking, when mathematicians refer to a complex number they mean a number that has two components, a sum of a real number and an (pure) imaginary. We say the number has a real part and an imaginary part. The complex number 7 + 6i has the two parts 7 and 6i. Seven is the real part, 6i is the imaginary part. And again, within a complex number, the imaginary part can be written with the i first.
The complex number 12 - 2i has real part 12 and imaginary part -2i, or -i2.
Here is a table with several examples that should clear up any questions you might have regarding the classification and understanding of all these different types of numbers.
Food for further thought?
What real-world meaning can be assigned to the quantity represented by an imaginary number, the square root of a negative number? What does it mean if a number cannot be represented by measurable quantities? What does it mean if a quantity is identified by unmeasurable numbers?
Understand that a negative (real) number does represent an amount. It is an amount that is missing. A deficit. You have -$10.00 in your bank account. That is an amount. A deficit amount. An amount that must be restored to your account.
The square root of a negative number cannot be represented by amounts that are measurable (positive or negative numbers). So what is the “reality” of an imaginary number, as we experience reality as something that our senses can observe and measure?
It turns out that complex numbers have been useful in physics. They often provide an easier path through a complicated mathematical calculation. However, if a calculation produces a final result that contains an imaginary number, it implies something that is not physically measurable. It is typically discarded, or viewed as an indication that our understanding of the phenomena being measured is incomplete, or perhaps wrong.
There is a historical tradition of new math discoveries, just like scientific revolutions, causing upheavals to the collective psyche of the reigning intelligentsia, and even personal tragedies. Ancient Greece records the untimely death of the mathematician who discovered irrational numbers. He purportedly died at sea… punished by the Gods.
Complex numbers play a significant role in the mysterious realm of quantum mechanics. With respect to the reality of imaginary numbers, it seems fitting that they are deeply ingrained into the mathematical framework used to describe the mysterious — some might say disturbing — behavior of light and sub-atomic particles in a quantum system. For more on this, check out this article from Mathnasium.
#
[1] Irrational numbers are those that cannot be represented as quotients of integers, that is, cannot be written as a fraction a/b. The most famous of which is π (pi), which is the ratio of a circle’s circumference to its radius.
The Author certifies this article is one hundred percent human made and that no AI was used in its production.



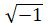
🤯